
As mentioned before, game theory assumes that the players are rational decision makers. Thus, based on the previous payoff table, a rational player will not use a lead-time strategy as an option for appropriation. This means that we can eliminate the lead-time strategy from the payoff table.
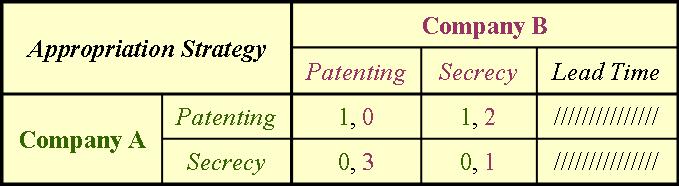
For Company A, a secrecy IP strategy is strictly dominated by patenting (1>0). Thus, a rational player will not use a secrecy strategy, allowing us to eliminate it from the payoff table.
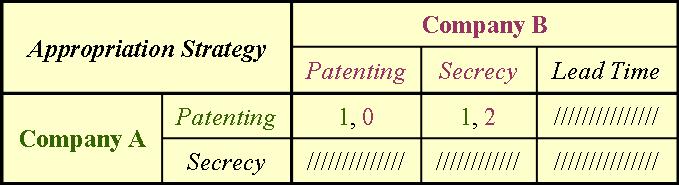
It is important to note again that with different payoffs, the outcome would be different. So, assumptions need to mirror reality as close as possible for such an exercise to be meaningful. This is a simple example of using game-theoretic approaches to analyze IP strategy. Iterated elimination of strictly-dominated strategies is one possible solution for non-cooperative static games. The analysis is more involved when one includes cooperation (or coordination) between players in which players communicate with each other regarding the acts they choose to perform, influencing the IP management decisions.
Another example involves a classic patent race to build up patent portfolios as a means of defense, and to create a perceived threat to expansion by a competitor. Consider two chemical or pharma companies who are rivals in an industry in which technology platforms are discrete, meaning that sales drop sharply when patent-term expiration occurs.
Both competitors consider massive growth of their patent activities to block entire technology spaces, and to reduce dependency on individual patents. Although patenting is very costly, each company concludes from a patent analysis they would benefit from stronger patent protection in the technology field. Each rival can individually decide whether to massively increase their patent activities, or to keep them at a low level.
In the hypothetical scenario, the possible outcomes for various IP strategy scenarios are:
- If only one company chooses to massively develop their patent portfolio, then the net present value (NPV) is estimated to be $500M for the company with the growth patent portfolio; whereas, the NPV for the company that chooses a cost-containment approach to patent activity by pursuing a low level of patent growth is estimated to be $100M.
- If both companies decide to massively develop their patent portfolios, then the NPV is estimated to be $200M for each competitor.
- If both companies decide to maintain a low level of patent growth, then the NPV is estimated to be $400M for each competitor.
In such a game construction, we have complete information in that the payoffs are known in advance. The game reflects simultaneous decision-making with an interdependency of strategies and payoffs. The payoff table for such a IP management patent race can be represented as follows.
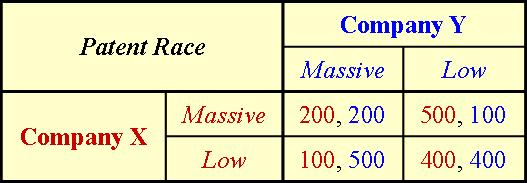
We can observe that, without cooperation, the ultimate outcome will gravitate to a situation in which both sides will choose to massively develop their patent portfolios – a form of arms race in the patent world. Such a situation is not desirable (at least not for the sake of the reasons described above), and resembles the famous prisoner’s dilemma – a classic non-zero-sum game as known in game theory.
If both companies behave “rationally” by choosing massive patent development, both will receive a modest reward (the “200/200” scenario). However, if both companies behave “irrationally” by choosing a low-growth patent strategy, both will receive a greater reward (the “400/400” scenario).
If players are allowed to cooperate (a type of interactive decision-making that is not strictly competitive), the solution is totally different. If both players agree to pursue a low-growth strategy, they will both benefit to a greater extent. In a broader IP context, such cooperation can include territorial restriction, covenants not to sue, patent pools, and open-source agreements – forms of détente in patent wars and global IP strategy.
The game can also be represented in extensive form (as with the infringement-litigation decision-tree) as follows.

Extensive-form analysis allows for multistage problems that have more than one decision point to be considered. Decision trees can be pruned at various decision branch points based on evaluated outcomes, simplifying the amount of calculation required in complex scenarios.
With such approaches, playing games with IP can provide valuable and surprising insight for IP management into how to formulate complex patent strategies for portfolio platform-positioning.

